第七章平面直角坐标系小结复习课件（30张）

本章回顾

本章我们通过具体实例学习了平面直角坐标系等知识，应用坐标方法解决了一些简单问题.

建立平面直角坐标系后，对于坐标平面内任意一点M，都有唯一的一对有序实数(x，y)和它对应;反过来，对于任意一对有序实数（x，y)，在坐标平面内都有唯一的点M和它对应．这样，我们就可以数形结合地研究问题.

坐标方法有广泛的应用．例如，我们可以利用坐标描述一些地点的分布情况;还可以通过直角坐标系中对应点的坐标之间的关系，研究图形平移等问题．这种用数和运算来研究几何问题的方法是非常重要的，今后我们将不断地看到它的应用.

交流预习

请你带着下面的问题，复习一下全章的内容吧.

1.在日常生活中，我们可以用有序数对来描述物体的位置．以教室中座位位置为例，说明有序数对(x，y)和(y，x）是否相同以及为什么.

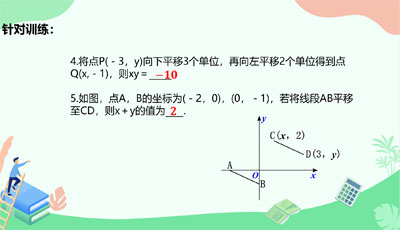
2.平面直角坐标系由两条互相垂直且有公共原点的数轴组成．请你举例说明如何建立平面直角坐标系，在直角坐标平面内描出点P(2，4）和原点的位置，并指出点Р和原点的横坐标和纵坐标. 平面直角坐标系的两条坐标轴将平面分成I，II，Ⅲ，Ⅳ四个部分，这四个部分依次称为第一象限、第二象限、第三象限和第四象限．请你在直角坐标平面内描出点A(2，1)，B(-2，1)，C(—2，一1)，D(2，一1)的位置，并说明它们所在的象限.

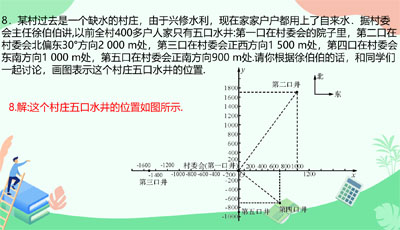
3.平面直角坐标系具有广泛的应用，请你举例说明它的应用.