知识梳理
1.二元一次方程(组)
含有_____未知数，并且含有未知数的项的次数都是___ 的方程叫做二元一次方程.
注意：
1.“一次”是指含未知数的项的次数是 1，而不是未知数的次数.
2.方程的左右两边都是整式.
方程组中有_____未知数，含有每个未知数的项的次数都是___，并且一共有两个方程，像这样的方程组叫做二元一次方程组.
二元一次方程组应同时满足三个条件：
(1)两个整式方程；
(2)方程组中一共含有两个未知数；
(3)含有每个未知数的项的次数都是1.
判断一对数值是不是二元一次方程组的解的方法 判断一对数值是不是二元一次方程组的解，只需将这对数值分别代入方程组中的每一个方程进行检验，若满足每一个方程，则这对数值就是这个方程组的解；若不满足其中任何一个方程，则这对数值就不是这个方程组的解.
3.二元一次方程组的解法
把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解．这种方法叫做____________，简称________．
三类代入消元法：
(1)直接代入：方程组中含有用一个未知数表示另一个未知数的形式的方程.
(2)变形代入：方程组中含有未知数的系数为1或-1的方程.
(3)整体代入：方程组中某一未知数的系数成倍数关系.
当二元一次方程组的两个方程中同一未知数的系数相反或相等时，把这两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程.这种方法叫做____________，简称________.
选用二元一次方程组的解法的策略
1.当方程组中某一个未知数的系数是1(或-1)时，优先考虑代入法.
2.当两个方程中，同一个未知数的系数相等或互为相反数时，用加减法较简单.
3.当两个方程通过变形用含有一个未知数的式子来表示另一个未知数都比较复杂时，往往选用加减法.
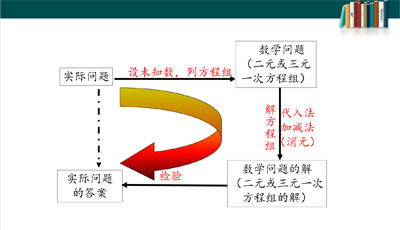
4.二元一次方程组的应用
根据实际问题列二元一次方程组的步骤：
（1）弄清题意；
（2）找准题中的两个等量关系；
（3）设出合适的未知数；
（4）根据找到的等量关系列出两个方程，并联立成二元一次方程组.
找等量关系的方法
1.抓住题目中的关键词，常见的关键词有:“比”“是” “等于”等；
2.根据常见的数量关系，如体积公式、面积公式等，找等量关系；
3.挖掘题目中的隐含条件，如飞机沿同一航线航行，顺风航行与逆风航行的路程相等；
4.借助列表格、画线段示意图等方法找等量关系.
5.三元一次方程组
方程组含有___个未知数，每个方程中含未知数的项的次数都是__，并且一共有三个方程，像这样的方程组叫做三元一次方程组.
三元一次方程组必须同时满足以下条件：
(1)方程组中一共含有三个未知数；
(2)含有未知数的项的次数都是 1；
(3)方程组中一共有三个整式方程.
